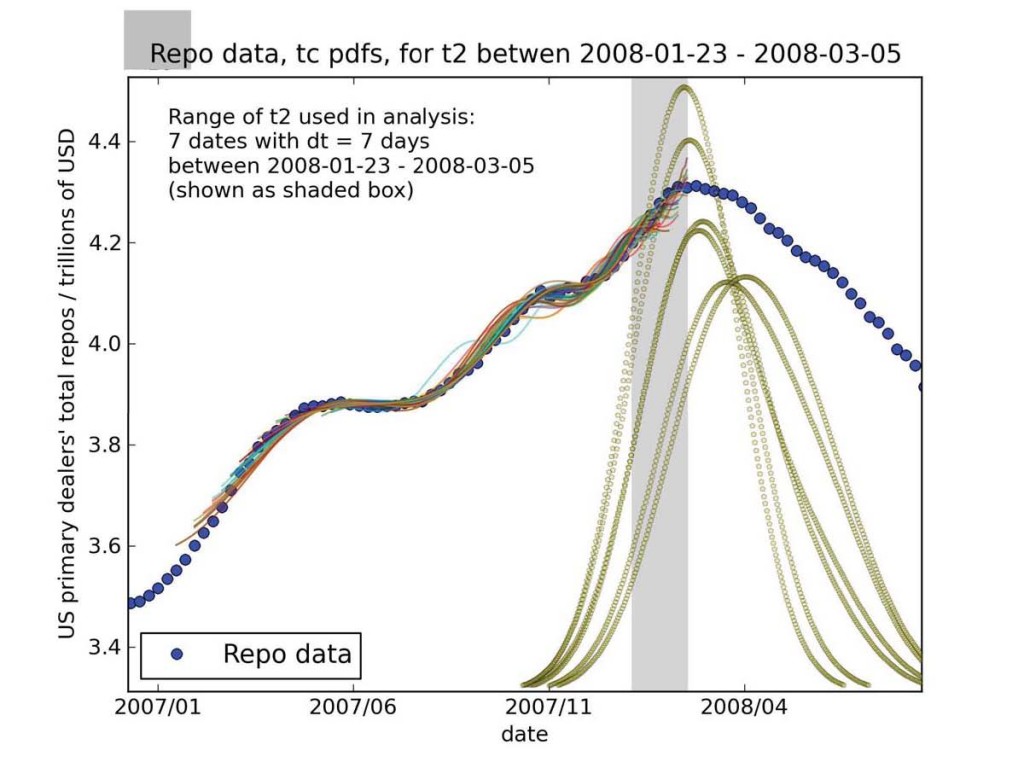
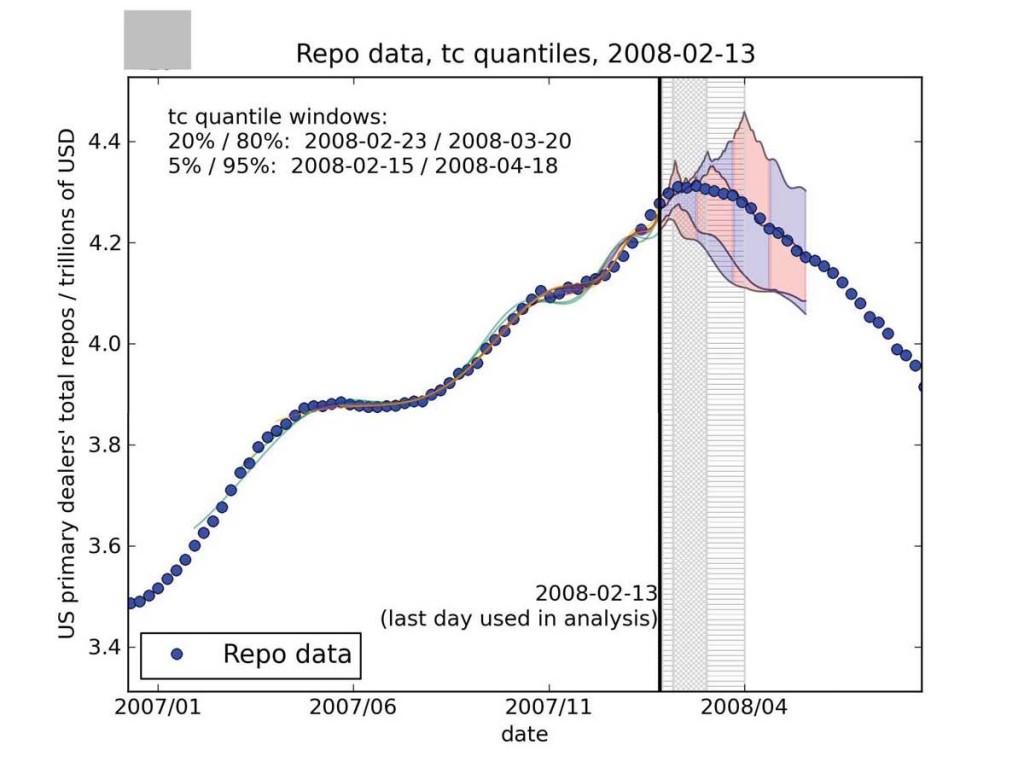
Instead of posting papers separately, I’ve decided to transition to a weekly reading list format. I’ll update this post over the course of the week, but here’s the initial list:
- Gelpern, Anna and Gulati, G. Mitu, Sovereign Snake Oil. Law and Contemporary Problems, Forthcoming.
- Chan, Kam Fong and Marsden, Alastair D.E., Empirical Tests on the Credit Default Swap and Stock Markets During the Global Credit Crisis.
- Friedman, Craig and Zhang, Yangyong, Estimating Flexible, Fat-Tailed Conditional Asset Return Distributions.
- Han, Bing and Zhou, Yi, Term Structure of Credit Default Swap Spreads and Cross-Section of Stock Returns.