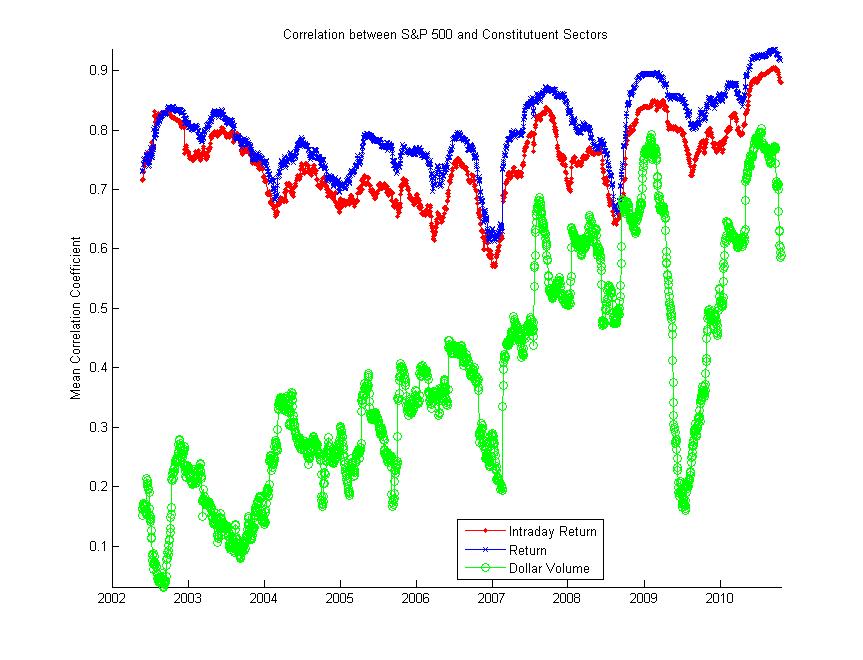
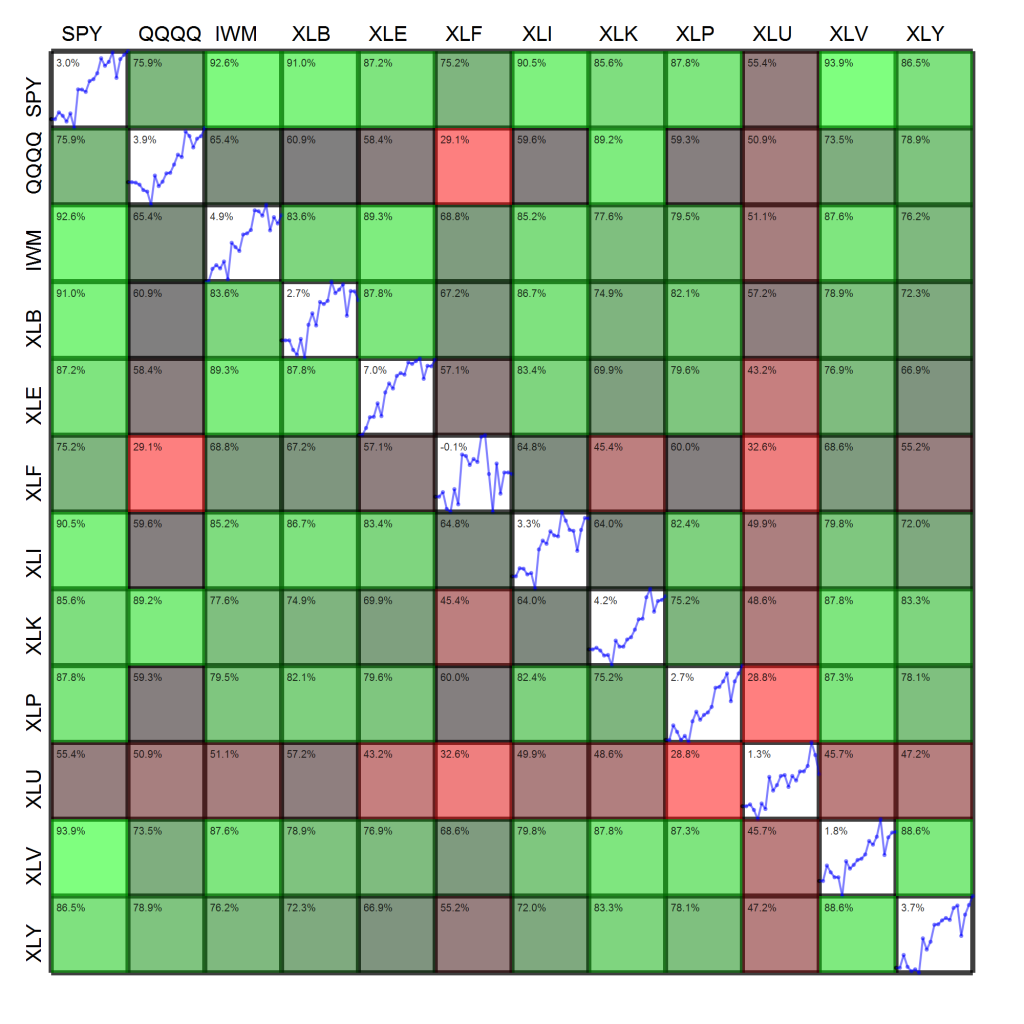
Here’s a paper out of the CabDyn group at Oxford from D. Fenn and M. Porter. Mason is also one of the leading researchers in network science, and their group has entered into a number of joint Ph.D./post-doctoral hires with the business school there. The result is a large number of interesting papers.  This particular paper investigates correlation matrices through RMT, which is exactly what my Quantitative Finance paper and recent working paper address.  Though they don’t examine their calculations in an applied context, the results provide additional view into recent correlation dynamics.  Abstract and download below:

Share/Bookmark

Here’s another new paper on q-FIN that I thought might be worth mentioning.  Having skimmed it, I have a few questions.  First, if the paper’s title includes the phrase “different time-scales,” you should include more than 15-minute interval sampling.  I’d like to see whether their conclusions are robust on two-minute or 60-minute intervals as well (like this).  Second, there is a large body of literature on the leading eigenvalues of the correlation matrix.  This path of inquiry is twenty years old and has already produced a number of the conclusions that are in the paper.  I guess I’m curious as to why they chose to use sum-of-signs instead of something like the proportion of the leading eigenvalue to the sum of eigenvalues (it works well here).   Anyway, even if there are some methodological issues, the paper’s conclusions are interesting and it’s always nice to see fresh work on intra-day dynamics and market “panic.”

Cross-sectional signatures of market panic were recently discussed on daily time scales in [1], extended here to a study of cross-sectional properties of stocks on intra-day time scales. We confirm specific intra-day patterns of dispersion and kurtosis, and find that the correlation across stocks increases in times of panic yielding a bimodal distribution for the sum of signs of returns. We also find that there is memory in correlations, decaying as a power law with exponent 0.05. During the Flash-Crash of May 6 2010, we find a drastic increase in dispersion in conjunction with increased correlations. However, the kurtosis decreases only slightly in contrast to findings on daily time-scales where kurtosis drops drastically in times of panic. Our study indicates that this difference in behavior is result of the origin of the panic-inducing volatility shock: the more correlated across stocks the shock is, the more the kurtosis will decrease; the more idiosyncratic the shock, the lesser this effect and kurtosis is positively correlated with dispersion. We also find that there is a leverage effect for correlations: negative returns tend to precede an increase in correlations. A stock price feed-back model with skew in conjunction with a correlation dynamics that follows market volatility explains our observations nicely.

L. Borland, Y. Hassid. Market panic on different time-scales. arXiv:1010.4917

Share/Bookmark